Si tuvieras que comprar un departamento como inversión, ¿Dónde lo harías?
La idea principal del trabajo será predecir, la localización del inmueble en el cual se obtendrá el mayor incremento en el precio, para el año siguiente, en base al reconocimiento de las variables que determinan que el incremento sea mayor a un umbral definido.
El umbral se definirá como el percentil 95.
Las bases fueron obtenidas de la web del Gobierno de la Ciudad y son las siguientes:
- Departamentos en venta de Capital Federal durante los años 2007 - 2015
- Centros de Salud Privado
- Centros de Salud y Acción Comunitaria
- Centros Médicos Barriales
- Comisarías
- Establecimientos Educativos
- Estaciones de Subte
- Estaciones de Metrobus
- Estaciones de Ferrocarril
- Clubes
- Hospitales
- Cuarteles y destacamientos de bomberos de Policía
- Paradas de Colectivo
- Dependencias Culturales
- Farmacias
- Universidades
Para el procesamiento se utilizó el lenguaje de programación R y se abarcó en tres etapas:
PRIMERA ETAPA
La primera etapa del proceso consistió en tomar las bases de los departamentos en venta del 2007 al 2015 para luego unificarlos en una sola base. Para ello, tomamos dichas bases y las filtramos por las columnas que tengan en común. Particularmente, para el set de datos de departamentos del 2015, los nombres de algunas columnas en común con el resto de las bases no coincidian completamente, por lo que fue necesario renombrar dichas columnas: como 'BARRIOS' por 'BARRIO', 'BAUL' por 'BAULERA', etc. para poder concluir con la unificación de estas bases.
Antes de unificar las bases, a cada una de las mismas le asignamos una nueva columna 'AÑO' que indique el año correspondiente de las ventas. Esto nos ayudará a saber de qué año es la venta del departamento en la base que generamos al unificar, ya que con el pasar de los años los precios van aumentando.
SEGUNDA ETAPA
La segunda etapa del proceso consistió en manipular cada una de las columnas del dataset generado anteriormente:
- Latitud y Longitud: En estas columnas filtramos vacíos y nos aseguramos que las coordenadas tengan la parte entera con dos dígitos y la parte decimal con al menos cuatro dígitos (con menos dígitos se perdía precisión y la ubicación ya difería en varias cuadras), ambas partes separadas por un punto. También se eliminaron los puntos que indicaban los separadores de miles, salvo el punto que separa la parte entera con la parte decimal, y se eliminaron las coordenadas erróneas (entre las mismas se detectaron latitudes de 4700 y otros números similares). Generalmente, las latitudes y longitudes de los datos tienen parte entera (-58.;-34.), por lo que nos guiamos con ambos valores, el resto lo consideramos erróneos.
- Terraza: Inicialmente se pensó que esta columna solamente indicaba con un SI o con un NO si el departamento posee una terraza, pero lamentablemente vimos que contiene diferentes valores como BALCON, PATIO, TERRAZA, SI, NO, PATIO Y TERRAZA, etc. o cualquier concatenación de estos valores. Para esto planteamos armar tres columnas nuevas: PATIO, TERRAZA y BALCON, para indicar si el departamento posee cada una de estas cosas por separado. Para llevar a cabo eso, se armaron dichas columnas a partir de un vector booleano que indica si la palabra 'BALCON', 'PATIO' o 'TERRAZA' forman parte del valor (string) en cuestión, marcando con 1 si posee o con 0 si no posee. De esta manera, por ejemplo, un valor como 'PATIO Y BALCON' va a asignar TRUE(1) tanto a la columna PATIO como la columna BALCON, ya que contiene ambas palabras.
- M2 (metros cuadrados): Acá además de filtrar los NA, también se filtraron aquellos departamentos que tengan menos de 14 metros cuadrados, ya que no tienen sentido.
- Dólares por metro cuadrado: Notamos algunos errores de tipeo, por ejemplo, se observó que algunos números decimales tienen un punto (que es lo correcto) mientras que otros tienen una coma (que fue necesario corregirlo).
- Dólares: Se observaron valores de 0 a 131 dólares, lo cual no tiene sentido esos precios para un departamento. Para corregir estos valores, en lugar de filtrarlos, los reemplazamos por el producto de su precio en dólares por metro cuadrado y sus metros cuadrados.
- Baños: Para el tema de los baños fue complicado, ya que se encontraron valores con NA, valores con 0 baños y valores mal tipeados con miles de baños. Decimos que fue complicado por lo siguiente: Por un lado, la cantidad de estos datos erróneos (sobre todo los de 0 baños) sumaban aproximadamente 40000 observaciones, casi la 3era parte de todo nuestro set de datos (que cuenta con unas 125000 observaciones), por lo que eliminarlos o filtrarlos era un grave problema debido a que se perdían muchos datos. Por otro lado, si reemplazábamos estos datos erróneos por una determinada cantidad de baños, por ejemplo por 1, vamos a tener el problema de introducir datos erróneos en gran cantidad de estas observaciones, ya que es muy factible que en 40000 observaciones hayan departamentos con más de 1 baño. A esto lo llamamos como el problema de los cero baños.
La solución a esto fue lo siguiente: Predecir la cantidad de baños en base a los metros cuadrados del departamento. Para ello se construyó un boxplot sobre los metros cuadrados en función de la cantidad de baños y de ahí sacar las conclusiones. De esta manera no nos aseguramos un 100% de aciertos pero sí la gran mayoría de ellos. A continuación se muestra el diagrama del boxplot en la que se estudió la cantidad de baños según los metros cuadrados de los departamentos:
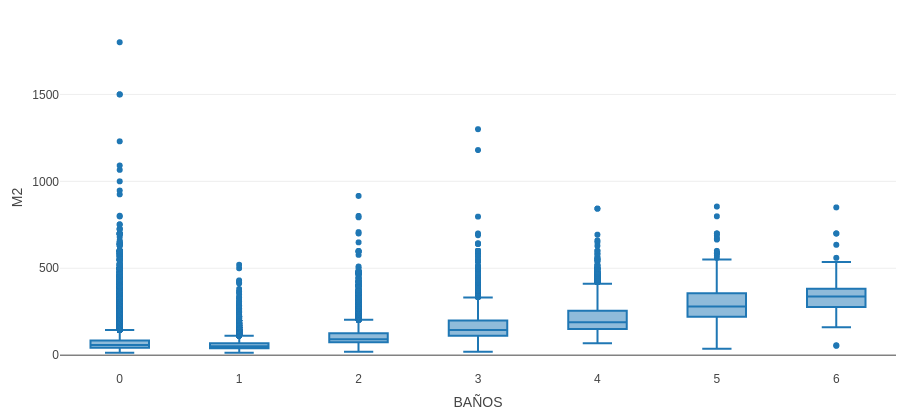
Este gráfico fué realizado con una librería de R que permite interactuar con el gráfico (que no es posible interactuar aquí por el hecho de ser solo una imagen), siendo muy util para observar los valores límite de cada caja. Lo que mostró el gráfico es que cada rango de metros cuadrados (M2) suele tener frecuentemente la siguiente cantidad de baños:
Entre 14 y 69: 1 baño.
Entre 70 y 118: 2 baños.
Entre 119 y 175: 3 baños.
Entre 176 y 238: 4 baños.
Entre 239 y 310: 5 baños.
De 311 en adelante: 6 baños.
Cabe destacar que en el set de datos, además de los 0 baños, mencionamos que también hubo unos pocos datos erróneos que marcaban desde los 7 a los miles de baños. Esto quiere decir que fue necesario establecer un límite superior a la cantidad de baños aceptables. Para ello, se investigaron aquellos departamentos de la ciudad que cuentan con la mayor cantidad posible de baños, a lo que se observó que no hay departamentos con más de 6 baños. Además, notamos que esto tiene sentido al observar el set de datos ya que cuanto más baños, menor cantidad de observaciones hay en el set, esto quiere decir que partiendo de 1 baño, la cantidad de observaciones iban diminuyendo cada vez más rápido hasta los 6 baños (con 350 observaciones aproximadamente), y luego en los 7 baños realizaba un gran salto (de 350 a unas 5 observaciones aproximadamente), concluyendo que allí se encuentra el tope máximo.
- Ambientes: Con los ambientes pasó lo mismo que con los baños, ya sea valores con NA, con 0 ambientes, con miles, etc. Aplicando el mismo método que hicimos con los baños, predecimos la cantidad de ambientes según el metro cuadrado mediante el siguiente boxplot:
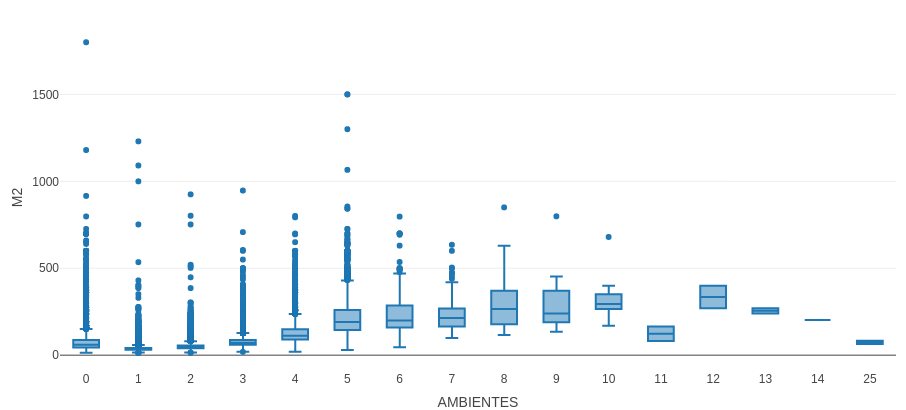
El gráfico de boxplot muestra que podríamos predecir hasta 6 ambientes, ya que con más ambientes tenemos pocos datos y probablemente erróneos, ya que hay departamentos de muchos ambientes con pocos metros cuadrados, la cual no tiene sentido. Con este gráfico se estimó la cantidad de ambientes para los siguientes rangos de metros cuadrados:
Entre 14 y 42: 1 ambiente.
Entre 43 y 59: 2 ambientes.
Entre 60 y 89: 3 ambientes.
Entre 90 y 149: 4 ambientes.
Entre 150 y 260: 5 ambientes.
Entre 261 y 285: 6 ambientes.
Para el resto de los metros cuadrados, es decir de 285 en adelante, los eliminamos ya que abarcan unos pocos cientos de datos.
- Barrio: No se encontraron valores NA pero sí algunos errores de tipeo que tuvieron que ser corregidos, como 'NUNES' por 'NUÑEZ', 'MONSERRAT' por 'MONTSERRAT', etc.
TERCERA ETAPA
En la tercera etapa del proceso se agregaron los puntos de interés cercanos a cada departamento, ya sean paradas de colectivo, subtes, trenes, farmacias, centros de salud, comisarías, etc. Esto nos dá una idea acerca de la ubicación de cada departamento, es decir si se encuentra en una zona céntrica o comercial o está alejado del centro, lo cual difiere en precio de las ventas. Para ello, se estableció por cada departamento un radio de 5 manzanas alrededor del mismo para luego observar los puntos de interés que caen dentro del área, representando los lugares cercanos al departamento. A continuación se ilustra un ejemplo sobre este planteo:
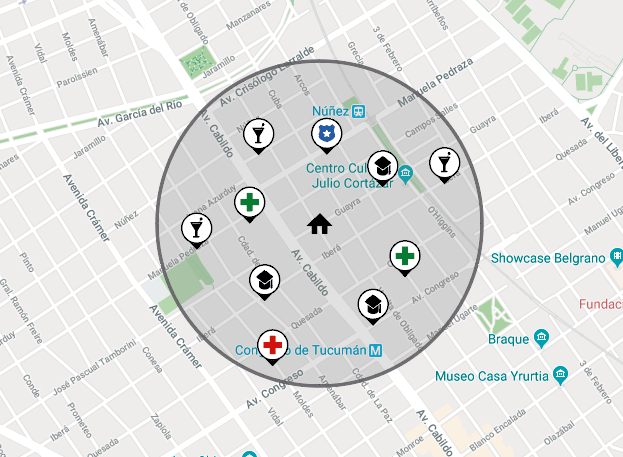
De esta manera, en el dataset, cada departamento tendrá una columna para cada punto de interés en la que indica la cantidad de cada uno de estos lugares dentro del radio de 5 cuadras, mostrando qué puntos de interés se encuentran cerca del departamento, a menos de 5 cuadras. Esto muestra una idea sobre la ubicación del departamento, ya que cuanto más puntos de interés se encuentren dentro del radio, más céntrica es la zona de ubicación.
Una vez finalizada el procesamiento de los datos, los agrupamos por Radios Censales. La idea principal de agrupar la base se debe a que, dado que vamos a comparar la variación del precio del metro cuadrado año a año, no vamos a poder contar con los mismos departamentos en cada año ya que hay departamentos que se venden mientras por otro lado surgen nuevos departamentos en venta. Debido a este motivo, la comparación se realizará entre distintos grupos.
Para ello contamos con una base de radios censales a partir de relevamientos de suelo que contiene información como latitud, longitud, ubicación, grupo, población, hogares, viviendas, etc. que será unificada con la base de las ventas de departamentos generada anteriormente mediante la longitud y latitud cuyos datos tienen ambas bases en común. De esta forma, la base de radios censales nos permitirá agrupar en 3371 grupos.
Una vez unificada las bases, agrupamos los datos por 'AÑO' y por 'GRUPO', y para cada uno de ellos obtenemos la media de los metros cuadrados, dólares, precio por metro cuadrado, ambientes, baulera, cochera, baño, lavadero, balcón, terraza y patio. En cuanto a la cantidad de lugares de interés cercanos, usamos la suma de los mismos para la agrupación.
Al obtener dichas agrupaciones, para cada grupo, sacamos la variación del precio por metro cuadrado año a año, y luego calculamos el promedio de las variaciones de los años 2007-2015. Usamos promedios debido a que hay varios grupos donde no tienen alguna de las variaciones anuales, por no tener departamentos en el grupo en alguno de los años observados.
Con la base ya agrupada, tomamos el promedio de las variaciones de los años 2007-2015, los ordenamos de forma decreciente y como en la introducción mencionamos definir el umbral como el percentil 95, tomamos el último 5% de todo el dataset (que corresponde a los promedios de variaciones más altos) y los reemplazamos por 1, mientras el resto (el primer 95% del dataset) los reemplazamos por 0. Estos reemplazos fueron llevados a cabo de esta manera debido a que esta variable será la que utilizará el modelo predictivo como valor de salida para predecir los valores (1 o 0), ya que los algoritmos de aprendizaje automático suelen predecir valores de 1 o 0, o un valor entre ambos.
Luego dividimos el data set en dos partes, uno para el set de entrenamiento que abarca los años 2007-2014, y otro para el set de pruebas que abarca el año 2015. El modelo utilizará el set de entrenamiento para ir entrenando o aprendiendo los datos mediante los valores de entrada (ambientes, baños, metros cuadrados, etc.) y los valores de salida (promedio de variaciones de precios), y luego, mediante el set de pruebas, predecirá el promedio de variaciones de precios del 2015 mediante los valores de entrada según el entrenamiento realizado previamente. Dichas predicciones serán comparadas con los valores reales de los promedios de variaciones del 2015 que ya disponíamos desde antes de armar el modelo para dar una idea acerca de la proximidad de los valores predichos con los valores reales mediante datos estadísticos.
Por último, corrimos el modelo usando random forest con XGBoost y realizamos diferentes muestras por cada modificación del modelo. En los mejores resultados se llegó a obtener hasta un 96% de precisión.
Ya obtenida las predicciones sobre el promedio de las variaciones del 2015, el último paso consiste en visualizar los resultados mediante un gráfico. Para ello se utilizó una visualización geográfica de la Ciudad de Buenos Aires en la que se indican las ubicaciones de los departamentos en venta que obtuvieron mayor aumento de precio por metro cuadrado, es decir, mayor promedio de variación. Esto se debe a que el barrio o zona donde se encuentran ubicados dichos departamentos se encuentran en pleno crecimiento y es muy factible que en los próximos años tengan mayores puntos de interés cercanos a cada departamento, lo que implica que aumente su precio. De esta forma, se lograría obtener una gran inversión al comprar un departamento que se encuentre en una zona en pleno crecimiento, como sugieren estos resultados.
Usando la visualización geográfica con la librería ggplot, se obtuvo el siguiente resultado:
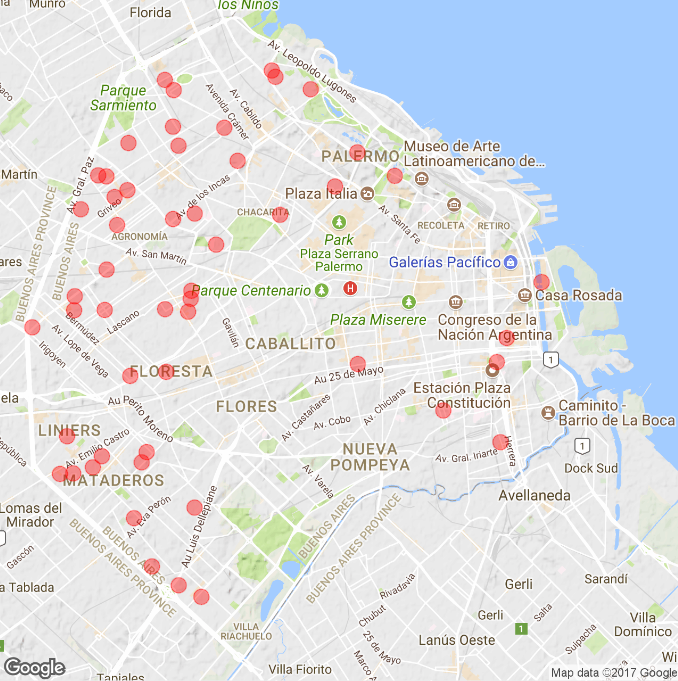
En la imagen se puede apreciar que los departamentos con mayor crecimiento en precio se encuentra en su mayoría tanto en el noroeste como en oeste de la ciudad, abarcando barrios como Villa Pueyrredón, Liniers, Mataderos y Villa del Parque, que según los resultados son los que se encuentran en pleno crecimiento.